Week 10: Sensitive Feature in RCoT

 1 Sensitive Feature in RCoT

The need for adding a parameter sensitive into RCoT algorithm is that, for data from reality, the variables always shows some degree of dependence, while the original RCoT algorithm is too sensitive to provide useful information, since it will regard all relations between variables as dependence.

Since the original result p-value goes to 0 when it detects dependence, which makes it impossible to modify it simply by adjusting the threshold, we would need to find another value to make the decision. The new value we use is Sta inside the RCoT algorithm, which is the number of samples multiplies the norm of covariance matrix of two variables.

1.1 Sta Property

Since we need a value which is unrelated with the sample sizes and the number of features, we need to adjust for original Sta to stabilize it on any situations, so that it can represents the degree of dependence between variables. Through experiments, we currently use Sta/(number_of_features**2), which is stable for different number of samples and features. It turns out it is still relevant with the number of conditions, where more conditions will result in smaller value.

Frankly speaking, using Sta does not have theoretical support, the whole purpose of it is to decrease the sensitivity of the original RCoT algorithm.

1.2 Implementation

Aside from calculate the new value Sta, we also need to adjust the output for it with new parameter sensitivity. The sensitivity decides the threshold for Sta about whether two variables are dependent. We also use tanh to translate the results into range [0, 1].

2 Conditional Expectation with ML

2.1 Implementation

Since the random forest shows best performance,  we now use it as our ML method to calculate expectation. For implementation, we also use parameter power to determine the number of trees of the forest. Larger power corresponds to more trees, which is consistent with the fact about power that larger power will have longer running time while provides more accurate results.

When test on it, some interesting fact shows that when conditioning on one variable, random forest's performance is poor compare with probability method, while conditioning on more than one variables, the performance gets better and shows large improvement over probability method. When conditioning on only one variable, we may need to use other ML methods or use D or J-Prob.

3 Plan for Next Week

• Merge the implementation into Because module
• Prepare for presentation and poster

Week 9: Experiment on Conditional Expectation with ML

 1 Conditional Expectation with ML

This week I mainly focused on doing experiments on conditional expectation with ML. The purpose of the experiments is to compare the performance between ML method and original implemented method (Discrete, J and U method, which utilizing RKHS), and between different ML algorithms.

1.1 Correctness of implementation

The first experiment was to test the correctness of the implementation, to see whether it can calculate expectation correctly.

The data model used and the experiments results are shown below:

The program are testing the ACE of IVA on IVC, which should be -3. We can see from the results that ML method can calculate correctly with the best accuracy.

1.2 Performance when increasing dimensions

The hardest part for calculating conditional expectation is that when dimensions go large, the dimensional curse occurs due to the sparsity of data. With high dimensions, the traditional discrete way to calculate expectation becomes infeasible since there are not enough data to give an accuracy estimation.

The experiments at this time try to show how the performance changes due to the increasing of the dimensions. The results are shown below:

Here we used Kernel Ridge Regression with Random Fourier Feature as our machine learning method. From the results above, we can observe that the average R2 (indicating how much the method has explained for total variance) decreases rapidly as the dimensions goes high. When running on 6 dimensions conditional, machine learning method seems to be unable to give a correct results, while J-prob method still shows good capability even with only 1000 samples.

1.3 Experiment with different ML algorithm

Since there are lots of ML methods for regression task, which has different properties, it is better to test all of them to say whether they have similar results regarding this task. The experiments results are shown below:

It turns out that different ML methods vary a lot in performance. K-Nearest Neighbor, SVM, Random Forest and Neural Network all show a better performance than J-Prob method. Especially for Random Forest, it outperforms other methods significantly with both 1000 or 10000 samples with very good runtimes.

Therefore, more experiments are done for RF algorithm to test out the best hyperparameter: the number of trees. The results are shown below:

From the experiments we can observe that the increasing of trees always shows a positive influence on the performance, while the price would be the increasing of runtimes.

2 Plan for Next Week

• Extend the conditional expectation with ML to discrete cases.

Week 8: Finish Direct LiNGAM and Start on Conditional Expectation with ML

 1 Direct LiNGAM

Last week we tried to unveil what behind Direct LiNGAM non-linear algorithm, and figured out what exactly happened for different cases. In this week, I tried to solve the last problem: What if the actual causal relation for x to y is y=f(x+e())? What will happen if we apply our algorithm on this structure? And can we detect this structure?

From the discussion last week, we know that this causal relation can be rewrite as x=f^(-1)(y)-e(). Since the mean of the noise e() is 0, this structure is exactly what we assume correct for causal relation. When I run algorithm on such cases, I would expect that the algorithm will give a reverse direction. However, in experiments, for both directions, the residual and variables are always detected dependently. Since the RCoT algorithm always gives 0 for dependency relationship, we need to find out a new method to evaluate the degree of dependency to determine the direction.

The value Sta we use is a intermediate value inside RCoT function, which is the sum of square of all value in the covariance matrix for Fourier Feature. A larger value would indicate a more strong dependency intuitively.

1.1 Function with no inverse function

It is still possible that the function doesn't have an inverse function. In this case, for both sides of the test, the residual will show strong dependency for both p-value and Sta would be similar and there is no way to determine the direction if only considering the dependency.

1.2 Function with inverse function

When running algorithm on functions with inverse function, like tanh or cubic function, the results turn out to fit our expectation. As we mentioned before that the p-value for both direction would all be close to 0, indicating that for both direction the residual show dependency with variable, which makes it hard to compare. However, when we use Sta to compare the degree of dependency,  we could see that in the backward direction there is less dependence, which fits our expectation that the algorithm will tend to give reverse results.

Since the algorithm for such case just gives out a totally reversed results, there is just no way that I can think of to distinguish between them.

1.3 Merge Request

The pull request for updating RCoT and integrating Direct LiNGAM non-linear has been merged into the Because module main branch.

2 Conditional Expectation with ML

This week I begin to work on this new topic.

By the end of this week, I have implemented the algorithm and run the simple test correctly.

The implementation basically follows other conditional expectation method, while replace the calculation of expectation into the machine learning prediction, and save the model in cache to reuse further.

Some little confusion about implementation arose and can be discussed in the meeting next week.

3 Plan for Next Week

• Discuss and optimize the current implementation
• Design test program to test the performance of conditional expectation.

Week 7: Insight into Direct LiNGAM Conjecture

 1 Direct LiNGAM Conjecture

In this week and last week, I spent some time digging into the exact non-linear cases for the direct test. More specifically, I visualized the fitting line and points to see how non-linear models work, and the relation between residual and variables to see whether the results fit our assumption.

After digging into the tests, I believe it is time to rethink on the conjecture and give a better illustration.

1.1 Basic Assumption

The basic assumption for Direct LiNGAM Conjecture is that it makes causal direction equivalent with the formula y = f(x) + e(), where f() can be any functions, and e() is a noise with mean 0 (if the mean is not 0, we can put the mean into f() and still get a mean 0 noise). In this case, if we detect a structure like this formula, then we will assume that y is caused by x.

We could notice that if the real causal effect does not satisfy our assumption, then the direct test could be totally wrong. For example, if the noise is relevant with x, or the noise is inside of the function f(), then we can not determine the causal direction correctly, since it is against our assumption.

1.2 Direct Detection

Now the question becomes how to detect such structure. We can notice that for the forward direction (the real causal direction), if we remove the influence of x from y, then the residual, which is the noise, is independent with x. Then in practice, we could fit y with x using a non-linear machine learning model, then run a independence test on the residual and x. If the residual is independent with x, then we could say that we discover a y = f(x) + e() structure.

Notice that we have a high demand on the non-linear machine learning model here, since we need it to remove all the influence of x on y. If the model can not fit the function f() well, then the residual will be dependent on x. Since there are a lot of choices for non-linear model, the through tests would be needed, which is done previously and viewed in visualization.

We could also think what will happen if the real causal doesn't fit out assumption. If the causal is like y = f(x) + e(x), where the variance of noise e() is dependent on x, then in our test, the noise will be dependent with x, and the correct direction can not be detected. If the causal is like y = f(x+e()), the residual we get will also be dependent on x. For example, if y = (x+e())^2 = x^2 + 2x*e()+e()^2, the residual we get will be 2x*e()+e()^2-E[e()^2], which is dependent on x. What's more, if we examine the backward direction, where x = f^(-1)(y)-e(). Then if the inverse function exists, like in this square case, the algorithm will detect that this backward direction is the correct causal direction.

Another question remained is that what if we run the direct test on the reverse direction if the causal effect satisfies our assumption. In fact it is the reverse case we discussed above, that x = f^(-1)(y-e()). The residual we get for this will be dependent on y (I am not quite sure about whether there exists a non-linear function where the residual will be independent with y, here different non-linear function and different kind of noise will have different results). If the relation is linear, then the noise can not be all from normal distribution, which has been proved previously, otherwise for both directions the independence will be detected.

Although in assumption we can detect such structure easily, in practice it may not be that easy since we don't have infinite dataset, and our non-linear model can not always fit the function well. And for some functions, it is just impossible to fit. Therefore, in practice we will run the direct test on both direction and compare the degree of independence. If the margin between two directions are large enough we will decide that the direction with more degree of independence to be the causal direction.

1.3 Non-linear Function Category

When visualization on the direct test results, it turns out that there are multiple cases of non-linear function, which have different results of the algorithm.

1.3.1 Non-monotonic Function

If the function f() here is non-monotonic, then there will be no inverse function, and the reverse direction will test out highly dependence. As long as we can fit the function well, the results would be correct.

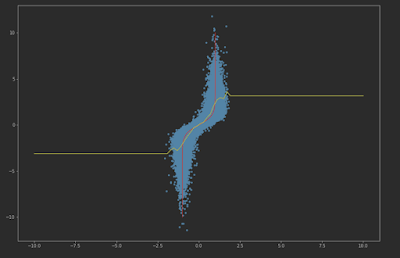
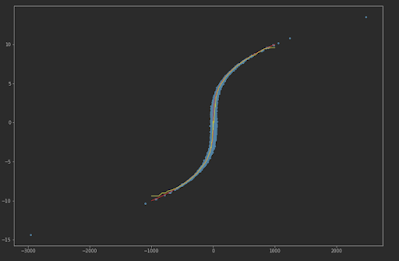
For example, we can visualize on square function, the results would be very clear.

Forward direction fitting line and residual

Backward direction fitting line and residual

1.3.2 Function Cannot Be Fitted

Some functions are just simply can not be fitted by a non-linear machine learning model, and for that causal direction, the residual will be dependent and the causal direct can not be detected.

For example, consider function y = 1 / x. If x comes from a noise with mean 0, the function just can not be fitted due to the extreme value.

Forward direction fitting line and residual

1.3.3 Function with 0 derivative in the limit

These functions are like the reverse version of hard-to-fit functions, where the inverse function of them is very hard to fit.

For example, we can consider the function y = tanh(x), where the derivative goes to 0 when x goes to infinite. The forward direction would be easy to detect. The backward direction would result in dependent results, though may not like what we expected that the residuals are dependent, but that we just simply can not fit the model.

Forward direction fitting line and residual

Backward direction fitting line and residual

1.3.4 Function Can Be Fitted

In the end we can examine the cases that the function can be fitted well by the non-linear model for both directions.

We can take y = x^3 as our example. We can observe that the residual in backward direction shows strong dependence on y, as we expected.

Forward direction fitting line and residual

Backward direction fitting line and residual

1.4 Integrating into Because

I rewrite the test_direction function in Probability Module and add self.power into cGraph class to support choice of direction test method. When using power>1, function would use non-linear model to fit, otherwise it would use LiNGAM tanh variant method.

For every test, the non-linear algorithm would run direction test for both directions and calculate the margin. If the margin is large enough, then we could decide that this direction is the correct causal direction. In order to output the results in consistency for both methods, the algorithm would scale the margin, then both methods would use 0.0001 as threshold.

Currently the non-linear method uses KNN (k-nearest neighbor) as non-linear model, and uses at the most 100000 samples to fit.

I also remove the standardize process in the algorithm, since I find that it has just input standardized data at the beginning. After test, it should accelerate about 10% of running time.

2 Plan for Next Week

• Begin working on conditional expectation with machine learning

Week 6: Direct LiNGAM

 Direct LiNGAM

Experiments on more non-linear models

More experiments done on non-linear models. The model of the data and the summary of the experiments are shown below:

We can draw conclusions from the results above:

• About correctness, all non-linear models show consistency. They all can not distinguish the direction on causal relation: (N, N3), with extreme value and hard to fit; (M, M4), the noise is related with the causal and can not detect independence; (M, M6), (M, M7), a reverse version of formula, the noise is on the other side of the direction, making the algorithm to draw the opposite conclusion; (IVB, IVA), normal noise which can not be distinguished by LiNGAM.
• The margin varies between models, Gaussian Process Regress has a better margin and good running time. Meanwhile, Kernel Ridge Regression with Random Fourier Feature are fastest, making it possible to applying on larger datasets. In such condition, KRR shows a best performance.

Experiments are also done to test the ability about noise with different variance. The model of data and the summary of experiments are shown below:

We can observe that:

• The correctness varies between models. However, in actual experiments, a lot of tests get margin around 0.05, which is exactly the threshold I set to determine the correctness. Therefore, it is very hard to say that the high correctness means the high accuracy, different runs may turn in different results, even if I run it 100 times every time.
• Using more data has significant improvement on the performance. Therefore, KRR with RFF has a lot advantage since it is a non-linear regression method and runs very fast.

Direct LiNGAM Conjecture

I made a jupyter notebook to visualize the results of the experiments above to look deeply into the Direct LiNGAM Conjecture. Since it is much more straightforward to see it using jupyter, I will leave a link to the notebook here instead.

Bug Fix

I fixed a bug when try to use RCoT on conditional dependence test. Before that, I didn't implement the conditional dependence test with RCoT. Since now RCoT becomes default method, this must be implemented.

I also fixed a bug about lpb4 algorithm. There is a chance that when running on very extreme condition, the lpb4 algorithm may occur a ValueError (The exact reason is inside the algorithm, which I am not familiar with). Now the algorithm will use hbe algorithm instead when that error occurs.

Plan for Next Week

• Presenting on Direct LiNGAM Conjecture and discuss it.
• Working on conditional expectation with ML.

Week 5: Still RCoT and LiNGAM

 RCoT

In the last week I integrated RCoT into the Because module, and Roger also finished his work on the traditional probability method on conditional probability. Then it is time to compare the performance.

RCoT vs Prob (Traditional Probability Method)

I run the experiments on two version of test datasets based on the original datasets. The first one is just the original one. In the second one I add more non-linear relationship to simple cases and remove non-linear relationship from the complex case.

I tried different value of Power, which is the parameter for Prob, and used default setting for RCoT, since from the experiments last week the results won't get improved if I increase the number of Fourier Features.

The results showed that:

• For Prob method, increasing Power won't change the results for whether a relation is dependent, it only improves a little for the margin between dependent and independent cases, and it increases running time linearly.
• The results for RCoT is better and more accurate than Prob in most cases, the margin is also larger.
• The running time for RCoT is similar to the running time for Prob when setting Power to 1, so basically Prob is always slower than RCoT.

Since RCoT has showed the better performance on both accuracy and running time, we have set the default dependent method to RCoT.

Downward Compatibility for Lower Version of Python

In the original implementation of lgb4 algorithm, it used math.comb function to calculate the number of combinations. However, it is only supported with Python 3.8 or higher version.

Therefore, I did a modification to it to support lower version of Python.

LiNGAM

Non-Gaussian Problem

It haunts me and Roger a long time why LiNGAM won't work on normal distribution, and in this week I tried to look into it and gave a reasonable answer to that problem from mathematical proof.

The basic idea is that:

1. We only consider the exact case in LiNGAM, which means the relation between all variables should be linear. And in this proof we only consider two variables where one causes another in linear relation, like y=w*x+noise().
2. Intuitively we think if we run linear regression on x with variable y, the coefficient would be 1/w, but actually we can prove that the coefficient should be w/(1+w^2).
3. Now we can explicitly write out the residual and y, we can prove that residual and y are independent if and only if the noise for both x and y are from normal distribution.

Develop New Direct Test Program and Data Model

I developed a new direct test program this week, which supports many runs with the same method at one execution. Each run will generate a new dataset based on the model provided. In the end the program will calculate the mean results for both forward and backward directions and the margin between them. In our expectation, the results for forward direction should be around 0.5 and the results for backward direction should be close to 0. A better method should have larger margin between them.

The new data model are shown below:

Basically we contained test cases:

• linear relation with normal and non-normal noise
• lot kinds of non-linear relation
• noise dependent on variable
• reverse version of relation
• linear and non-linear combination of multiple variables

Experiment on Different Regression Methods

The different methods tested and their running time table are below:

I also run all methods on 1000 samples with 10 runs to see the accuracy. The conclusions are:

• LinearRegression or any kinds of linear model are totally limited on linear relations, which is expectable. Though they have the fastest speed, it is very hard to apply it in practice due to their limitations.
• The other non-linear regression model share very similar results in experiments. They made mistakes on (N, N3) pair, where they all can not fit well due to it extreme value around 0. They made mistakes on (M, M4), which is expectable since now the noise are dependent with M. (IVB, IVA) is incorrect since the noises are normal. The results for (M, M6) is reversed which is exactly what we expected. The only difference is on (EXP, EXP5), which is complex and some model can give correct results.
• The running time varies a lot. Overall, I think Ridge Regression with Random Fourier Feature has the best performance on speed and can correctly test the results as expected.

Non-linear Regression

In the LiNGAM algorithm, when we want to extend the algorithm to non-linear relation, we must use non-linear regression methods. In the future work on using machine learning to estimate conditional expectation value, non-linear regression is also required. Therefore, it may be better to understand all non-linear model, how they learn from data, what kind of property they have, in order to choose the better one from them.

Therefore, I will start to learn the basic idea of them, and take some notes here.

Kernel Ridge Regression

KRR (Kernel Ridge Regression), just like its name, combines both kernel function and ridge regression. It first uses kernel function to map the original data to a feature space, then uses ridge regression to learn a linear function with L2 penalty. When we use non-linear kernels, we can get the non-linear function in the original space.

So in fact the KRR is very similar to SVR (Support Vector Regression). The only difference would be the loss function. KRR uses traditional linear loss, least squired error, while SVR uses an e-insensitive loss, which ignore the cases where the error is less than a threshold e.

Therefore, the KRR would train faster than SVR, while SVR will predict faster since it only use part of training samples to predict. (The KRR implemented in sklearn and in rff implementation are different, which may be the reason for the different running time.)

Support Vector Regression

The property of SVR is that it ignores the cases that have the prediction error less than a threshold e, and only try to fit on the hard cases.

Plan for Next Week

• Keep working on LiNGAM to compare non-linear method and its boundary.
• Start with the machine learning method on estimation of conditional expectation.

Week 4: Finish RCoT and Begin with DirectLiNGAM

 1 RCoT algorithm

1.1 Experiment and deal with R parameter

In the last week, I did some experiments on R parameter, and the results were fully against our intuition. Therefore, in this week, my first job is to examine why this results occurred.

It turns out that the only use of the parameter R is to determine how many samples to use to calculate the median of distances between all samples. When R is set to all samples, we give the actual median of distances. When R is less than the total number of samples, we give an approximation of median based on R samples. The median of distances will be used to determine the scale of parameter W in Fourier Random Features. Larger distances result in smaller W, which increases the frequency of the cosine function to generate more fitted Fourier Features.

The problem behind this is that, in fact, we will normalize every variable at first. Therefore, the median of distances is always close to 1. In experiments, the distances vary from 0.8~1.2. Then there are no benefit for us to set larger R, which will not improve the approximation of median of distances but only increase the running time.

What's more, I could also directly set the approximation to 1. In experiments, this action didn't impact the results but improve the running time a lot. In fact, the part of calculating distances is the most time consuming part in the algorithm. When I remove it from the algorithm, the algorithm's running time decreases dramatically.

In the current version of RCoT algorithm, I set approximation to 1.

1.2 Experiment and deal with the number of Fourier Features

After remove the influence of R parameter, it is possible to experiment on the parameter which determine the number of Fourier Features.

It turns out that even with 2 conditional and non-conditional features, the algorithm begins to have the ability to test direct linear relation correctly. But it is hard to detect conditional dependence.

With 5 conditional and non-conditional features, it begin to have the ability to detect more complicated relation, and can detect direct relation accurately.

When set conditional features to 25, the algorithm can detect linear dependent accurately, and from that, the algorithm won't improve much even we set conditional features to 500 and non-conditional features to 50 (in this setting, the running time is much longer than before we have not remove parameter R). 

It turns out that increase the number features has limited influence on the accuracy of the algorithm. It will benefit the algorithm when the number is small at first, but when it is over some threshold (25 and 5 in this case), the benefit stops. The algorithm can always correctly detect linear relation, but has errors on non-linear relation no matter how large we set the number of features.

Above are the examples of non-linear inverted V structure that the algorithm can never detect correctly.

1.3 Integrate RCoT algorithm into Because module

The Pull Request has been created and merged into the main branch of Because.

Basically it adds a new method for dependence test and enable the independence test program to test on RCoT algorithm.

2 DirectLiNGAM

2.1 Improve Direct Test program

In order to test the direct detection ability of the DirectLiNGAM and to compare different methods., it is important to create a lot of conditions and examples to test the boundary of their ability.

Now the Direct Test Dataset has SEM:

Which include cases:

• linear and non-linear relations
• normal and non-normal noises
• large and small noises
• monotonically and non-monotonically relations

Further cases can be added:

• More complex relation between more than 2 variables
• larger and smaller noise to find the detect boundary

Direct Test is done on both direction for every relation to test the ability of detect direction.

2.2 Implement DirectLiNGAM non-linear variant

In the original DirectLiNGAM method, it only uses a linear regression, so it doesn't have the ability to detect non-linear relationship. For example, if the actual relation is a square function, then the residual is highly correlated with variables and the direction can not be detected.

Now, if we use non-linear regression method, then it is possible that we can extend the LiNGAM algorithm into non-linear condition.

The choice of non-linear regression method is a lot, and now we just use SVM method to test the possibility. More methods and experiments are needed to be done.

Above are the code and the results. The code is very straight forward. We do a regression first, get the residual and run RCoT on variable and residual to test the dependency between them. If RCoT return a p-value close to 0, then it detects a strong dependency between them, which means the current direction should be wrong if we assume that the relation is like y = f(x) + e, where f(x) is a non-linear function. If p-value are not close to 0, then the residual and the variable could be independence, and the direction could be true.

From the preliminary experiments we can observe that for these simple examples (just direct relation and fit the assumption we make about the relation, which is y = f(x) + e), the algorithm can detect direction correctly for all kinds of non-linear and linear examples, except for 3 cases:

• N and N3: it may be too hard for SVM to regression on N3 = 1/N since it goes too large around 0.
• IVA and IVB: it is normal noise for both variables (the reason why normal noise can not work should be looked into in the future, I also don't quite understand much)
• EXP and EXP2: Hyperbolic Tangent function or exponential noise may be the reason. (additional experiments have done on these and in this time the algorithm detect correctly. Additional relation has set for exponential distribution and turns out the algorithm can detect direction with exponential noise.)

Further experiments should be done on it to test:

• more non-linear regression method
• more non-linear relation
• more complex relation consisting of multiple variables

Since the data generating process and RCoT algorithm have randomness, it is also important to run multiples times on different dataset with the same setting to eliminate the randomness. A through test program is under development.

3 Bug Report

When I try to compare RCoT algorithm and traditional prob method on dependency test, I encountered an error:

It turns out that when running conditioning on two variables, the Subspace gives 0 data:

I tried looking into filtering function but I don't actually understand how it worked.. So I don't know why it happened.

4 Plan for Next Week

• Develop the direct test program
• Do experiments on different method mentioned above thoroughly
• Look into the problem mentioned above, like the normal noise